RSA Encryption

RSA is like putting information into a locked mailbox. Anyone can encrypt, but only the person with the key can open and read its contents.

Setting up our encryption / decryption system

Before we start sending messages, we need to do some setup. We need to establish a system that allows us to encrypt and decrypt.

1. First, we arbitrarily pick a set of primes $p$ and a $q$ and we set $N = pq$. Often times, $p$ and $q$ are very large (512 bits each) and we don't want the hacker to know them.

2. Second, we pick an encryption key $e$ relatively prime to $(p-1)(q-1)$.

Our public key, something we distribute to anyone, is $(N,e)$. With these two numbers, anyone can have the power to encrypt information into a specific format only we can decrypt.

3. Now we derive a decryption key. We don't want the hacker to know this number!

Note, that $e$ and $d$ are derived in $\mod{(p-1)(q-1)}$. The reason will become more apparent later in the proof. The decryption key is the inverse of the encryption key, which is astronomically hard for a classical computer to create without knowing $p, q$. This decryption key is kept only for us to know.

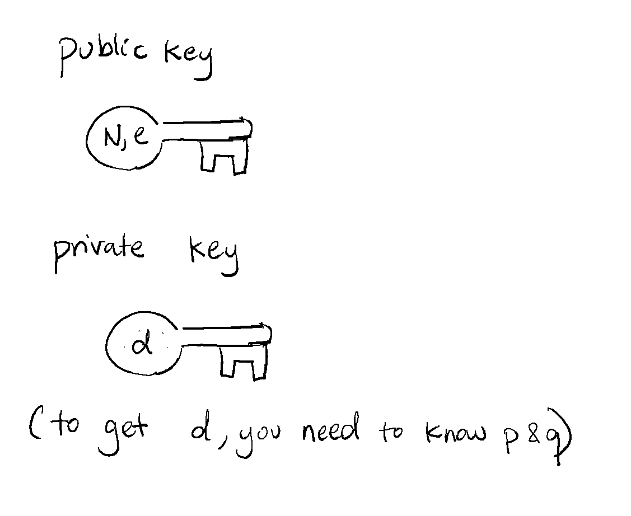
To recap, we have our public and private keys!

Encrypting / Decrypting Messages

Let's say we have a message $x$ in the modspace of $N$.

• Encrypting: $x^e \mod{N}$ is our encrypted message
• Decrypting: $(x^{e})^{d} = x^{ed} \mod{N} = x \mod{N}$ is our decrypted message

It's that simple! Just by using $\text{message}^{\text{encryption key}}$, we have our encrypted message. And with $\text{received message}^{\text{decryption key}}$, we'd have our original message! We use modspace because computers have finite memory.

Why does this work?

We've setup our system such that:

• $ed \equiv 1 \mod{(p-1)(q-1)}$
  • This is because our setup:
    • $d = e^{-1} \mod{(p-1)(q-1)}$
    • $e \mod{(p-1)(q-1)}$

Using this property we can rewrite the expression above as (will come in handy later):

• $ed = k(p-1)(q-1) + 1$

We can use the previous relationship to rewrite the message after applying a decryption key:

• $x^{ed} \equiv x^{k(p-1)(q-1) + 1} \equiv x \mod{pq}$

In this form, we can reduce using the following.

• $x (x^{k(q-1)(p-1)}) - x \equiv 0 \mod{p}$
  • If $x$ is not a multiple of $p$, then we can use Fermat's Little Theorem to reduce the expression.
    $$x ((x^{k(q-1)})^{p-1} - 1) \equiv 0 \mod{p} \\ x (0) \equiv 0 \mod{p}$$
  • If $x$ is a multiple y $p$, then expression reduces to $0$ by definition
• $x (x^{k(p-1)})^{(q-1)} - x \equiv 0 \mod{q}$
  • By symmetrical argument as above.

It is divisible by both $p$ and $q$ invididually. Since $p$ and $q$ are primes it must be divisible by their product, $pq = N$