Error Correction Codes

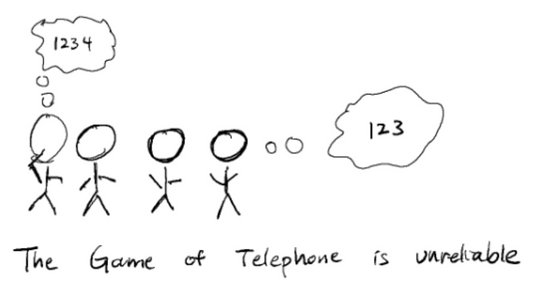
How do I ensure my message get's delivered correctly given that someone might tamper with it?

Erasure Errors (Someone erases parts of our message)

Imagine someone erases parts of our message. How do we prevent that?

Step 0 - Setup

Your packets will come in pairs $(index, message)$ where the $message$ is in modspace of a prime. A simple example is $(1, 7)$ in $\mod{31}$ .

You may notice that these messages oddly look a lot like $(x, y)$ coordinates on a Cartesian plane. It may be helpful (in order to get a first initial grasp of things) to think of them as $(x,y)$ points on a $xy$ plane that is finitely large.

Notice a pattern:

Two points defines a 1st degree polynomial ( $a_1 x + a_0$ )
Three points defines a 2nd degree polynomial ( $a_2 x^2 + a_1 x + a_0$ )
Four points defines a 3rd degree polynomial ( $a_3 x^3 + a_2 x^2 + a_1 x + a_0$ )

\text{More formally, $d$ points uniquely identify a $d-1$ degree polynomial.}

If we have the polynomial, we have the packets. As long as you receive more than or equal to d points, then you can recreate the $d-1$ degree polynomial.

\text{Hence to combat $k$ erasure errors, we can just send at least $d + k$ points to recover our polynomial.}

Step 1 - Lagrange Interpolation

The point of Lagrange interpolation create a $d-1$ polynomial from the $d$ points. In order to send $d+k$ points, we need $k$ extra points. To find $k$ extra points we need the unique polynomial, which we use lagrange interpolation for.

Say our message is $736$ . Our packets are: $(1, 7), (2, 3), (3, 6)$ . Since the values are small, we'll choose modspace 11.

We can define a new variable and fit it into the following form:

\begin{align*} \Delta_1 &\equiv \frac{(x - 2) (x - 3)}{(1 - 2) (1 - 3)} \equiv \frac{(x - 2) (x - 3)}{2} \equiv 6 (x - 2) (x - 3) \mod{11} \\ \Delta_2 &\equiv \frac{(x - 1) (x - 3)}{(2 - 1) (2 - 3)} \equiv \frac{(x - 1) (x - 3)}{-1} \equiv 10 (x - 1) (x - 3) \mod{11} \\ \Delta_3 &\equiv \frac{(x - 1) (x - 2)}{(3 - 1) (3 - 2)} \equiv \frac{(x - 1) (x - 2)}{2} \equiv 6(x - 1) (x - 2) \mod{11} \end{align*}

Notice that for all indexes other than its own, it reduces to zero. Notice that for its own index, it reduces to one.

This important relationship allows us to write our polynomial in the following form:

\begin{align} f(x) = m_1 \Delta_1 + m_2 \Delta_2 + m_3 \Delta_3 \mod{p} \end{align}

Hence our ultimate polynomial is:

\begin{align*} f(x) &= 7 \Delta_1 + 3 \Delta_2 + 6 \Delta_3 \mod{11} \\ &= 9(x - 2)(x - 3) + 8(x - 1)(x - 3) + 3(x - 1)(x - 2) \mod{11} & \text{Using modulus arithmetic} \end{align*}

We have our polynomial! If we plugin 1, 2, or 3, we'll receive our original message of 7, 3, and 6!

Step 2 - Create extra points

Now that we have the polynomial $f(x)$ that goes through all our points, we can create $k$ extra points by plugging in more indices to our function. So if there are at most two erasure errors, we can add $(4, f(4))$ , $(5, f(5))$ to our original message.

\text{message: } (1, 7), (2, 3), (3, 6), (4, f(4)), (5, f(5))

Step 3 - Send message over noisy channel

Here, someone might erase parts of our message.

\text{message: }(1, 7), (4, f(4)), (5, f(5))

Step 4 - Recover using Lagrange Interpolation

We reuse Lagrange Interpolation to recreate the polynomial and find the message values for indices $2$ and $3$ .

\text{...Lagrangian Interpolation} \\ f(x) = ... \\ \text{message: } (1, 7), (2, f(2)), (3, f(3)) \\ \text{message: } (1, 7), (2, 3), (3, 6)

We've recreated our message. Information was preserved.